-
Notifications
You must be signed in to change notification settings - Fork 273
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Feature Request: Binomial Coefficient Entropy Coding for Inverted Index Postings #329
Comments
|
I am familiar with this approach. I have actually implemented something similar in the past. The challenge is in providing an efficient software implementation. Binary interpolative coding can be implemented reasonably efficiently. A library like BitMagic has a good implementation. It is an interesting question to determine whether your proposal can be implemented reasonably quickly. |
|
Thank you for your response. Honestly, I appreciate your reply. Forgive me for asking but is there an encoding-decoding benchmark. Perhaps a collection of sequences? I was planning on releasing an MVP built with logarithms and I would love to test my implementation on some data. Forgive me for bothering you. |
|
@MurageKibicho Maybe https://github.com/RoaringBitmap/real-roaring-datasets could help? |
|
Thank you! |
|
These are my reasonably fast decoding implementations without any optimizations. These tests were ran in my dorm room on a simple laptop with 8 Gib of ram without a dedicated graphics card. Implementation DetailsThere are two implementations. Both are based on the lexicographic ordering of integers. The first method works recursively somewhat like Pascal's triangle. It is the fastest. It uses a for loop to generate the next possible lexicographic ordering from the previous one. Test DetailsWe use the integer range 0 - (28 choose 20) = 3108104. This range can be interpreted as a collection of all possible inverted index sequences of length 20 with a maximum possible value less than 28. The total number of integers in this range is (20 * 3108105) = 62162100. Sample Data: Test ResultsMetrics:
#Single For Loop To Create Dictionary Implementation #include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "SharedLibraries.h"
//gcc SharedLibraries.c PostingsLookupTable.c -o main.o && ./main.o
/*
File Name: PostingsLookupTable.c
Role: Creates one lookup table to find the combination represented by a number n
Note: NchooseK is called once, then a for loop is used to create the entire table
*/
/*
Function: CopyArray
Input: int *source, int *destination, int length
Role: Copies source array to the destination
Note: This is where the conversion happens
*/
void CopyArray(int *source, int *destination, int length)
{
int start = 0;
for(int i = length-1 ; i >= 0; i--)
{
destination[start] = source[i] + start;
start++;
}
}
//This algorithm is discussed in the Docs under technical details
//eg 0000 = 1000, 2222 = 3000long NchooseK(int n, int k)
/*
Function: GenerateLookupTable
Input: int *source, int *destination, int length
Role: Copies source array to the destination
Note: This is where the conversion happens
*/
int **GenerateLookupTable(int maxValue,int arrayLength)
{
long max = NchooseK(maxValue + arrayLength, arrayLength);
int *current = calloc(arrayLength, sizeof(int));
int **result = malloc(max * sizeof(int*));
for(long i = 0; i < max; i++)
{
result[i] = malloc(arrayLength * sizeof(int));
CopyArray(current,result[i],arrayLength);
for(int j = arrayLength-1 ; j > 0; j--)
{
if(current[0] == current[arrayLength-1])
{
current[0] += 1;
for(int j = 1; j < arrayLength; j++)
{
current[j] = 0;
}
break;
}
if(current[j] != current[j - 1])
{
current[j] += 1;
for(int k = j+1; k < arrayLength; k++)
{
current[k] = 0;
}
break;
}
}
}
free(current);
return result;
}
void DestroyPostings(int **postingsTable, long dataCount)
{
for(long i = 0; i < dataCount; i++)
{
free(postingsTable[i]);
}
free(postingsTable);
}
//How to use sample
int main()
{
//Note maxvalue is the expected size of n for n choose k
int maxValue = 8;
int sequenceLength = 20;
long dataCount = NchooseK(maxValue + sequenceLength, sequenceLength);
int **postingsTable = GenerateLookupTable(maxValue,sequenceLength);
clock_t start = clock();
for(int i = 0; i < dataCount; i++)
{
//printf("%d: ",i);
//PrintArray(postingsTable[i], sequenceLength);
}
clock_t end = clock();
printf("Time: %f",(double)(end-start) / CLOCKS_PER_SEC);
DestroyPostings(postingsTable, dataCount);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
//gcc RangeDivision.c -o main.o && ./main.o
/*
File Name: RangeDivision.c
Function: NchooseK
Input: int n, int k
Role: Calculates the binomial coefficent(n,k) up to 64 bits
*/
long NchooseK(int n, int k)
{
long result = 1;
if(n < k)
{
return 0;
}
if(n == k)
{
return 1;
}
if(k > n-k)
{
k = n - k;
}
for(int i = 0; i < k; i++)
{
result *= (n - i);
result /= (i + 1);
}
return result;
}
/*
Function: IntegerToPostings
Role: Finds the bitmap that corresponds to an integer using Range Division, like Arithmetic coding
Inputs: integer - this is our encoded value
minRange - always 0. This is the minimum value in our list
maxRange - NchooseK. This is the maximum binomial coefficient
zeros - number of zeros for our bitmap output
ones - number of ones for our bitmap output
postings - array to hold bitmap
currentLength - starts at 0. Increases by 1 at each recursive call
wantedLength - the length our bitmap output should have
*/
void IntegerToPostings(long integer, long minRange, long maxRange, long zeros, long ones, int *postings, long currentLength,long wantedLength)
{
double total = (double) zeros + (double) ones;
long zeroMaxRange = minRange + (long) ((double) (maxRange - minRange) * zeros / total);
//printf("%ld %ld %ld %.0f\n", maxRange,minRange,zeros,total);
if(currentLength == wantedLength)
{ //Base case
return;
}
if(integer <= zeroMaxRange)
{
postings[currentLength] = 0;
zeros--;
currentLength++;
IntegerToPostings(integer, minRange, zeroMaxRange, zeros, ones, postings, currentLength, wantedLength);
}
else
{
postings[currentLength] = 1;
ones--;
currentLength++;
IntegerToPostings(integer,zeroMaxRange, maxRange, zeros,ones, postings, currentLength, wantedLength);
}
}
void PrintArray(int *array, int length)
{
for(int i = 0; i < length; i++)
{
printf("%d", array[i]);
}
printf("\n");
}
int main()
{
//We want to output a bitmap of length 28
int zeros = 8;
int ones = 20;
int binaryLength = zeros + ones;
int *postings = calloc(binaryLength, sizeof(int));
long total = NchooseK(zeros+ones,ones);
//This is a loop through all integers between 0 and 28choose20
clock_t start = clock();
for(int i = 0; i < total; i++)
{
//printf("%2d ", i);
IntegerToPostings(i+1,0,total,zeros,ones,postings,0,binaryLength);
//Note our output is a bitmap that is read from right to left - The rightmost value is index 0
//PrintArray(postings, binaryLength);
}
clock_t end = clock();
printf("Time: %f",(double)(end-start) / CLOCKS_PER_SEC);
free(postings);
return 0;
} |
Summary
This is a proposal for encoding inverted index integer sequences using a number system based on binomial coefficients.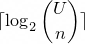
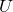 is largest number in the list and
is largest number in the list and 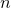 is the number of elements in the list.
is the number of elements in the list.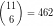 and
and
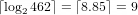 .
.
This number system is chosen because the minimum number of bits needed to encode a list of strictly increasing integers
is given by the equation
where
For example to encode the sequence 1,2,3,4,10,11 we need at least 9 bits:
Binary interpolative coding, one of the best methods for inverted list compression takes at least 20 bits to represent the example sequence. You can confirm this here.
However, if we represent the same sequence as a sum of binomial coefficients, it takes 10 bits to encode the list, and an extra 3 bits to store the length of the list. The total is 13 bits. You can confirm this here.
Motivation
Compression is a solved problem. The best compressors work by changing radixes, or number bases to find the most concise representation of data.
For instance, arithmetic coding is a generalized change of radix for coding
at the information theoretic entropy bound. This bound is a measure of redundancy - how many duplicates are in your data. Strictly increasing integer sequences have no duplicates, therefore, cannot be compressed
according to the information theoretic bound. This means huffman coding and arithmetic coding methods are inefficient with non-repetitive integer sequences.
This rfc proposes the use of the combinatorial number system to encode inverted index integer sequences at the combinatorial information theoretic entropy bound.
Just like arithmetic coding, this change in number systems allows us to encode integer sequences with the least number of bits.
I am a Math major in my junior year and if this RFC succeeds I would love to take a gap year and work on this library full time. The library
has sample code for converting between binary and the combinatorial number system using a greedy algorithm, or by generating a lookup table.
Technical design
Overview of Combinatorial Number System
Any natural number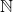 can be uniquely written as a sum of binomial coefficients
can be uniquely written as a sum of binomial coefficients
using this greedy algorithm.
Example: Find the combinatorial representation of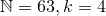
To reverse the process, sum your list of binomial coefficients
Comparison to Binary Interpolative Coding
In the example above, it can be seen that the sequence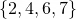
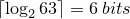 using the combinatorial number system with an extra 3 bits to store the length of the sequence. This is a total of 9 bits to encode this sequence.
using the combinatorial number system with an extra 3 bits to store the length of the sequence. This is a total of 9 bits to encode this sequence.
can be encoded in
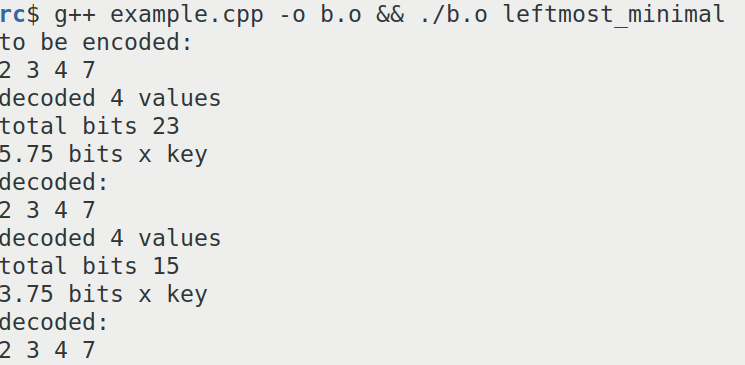
Using this library it can be confirmed that binary interpolative coding takes between 15 to 23 bits to encode the same sequence.
This is a screenshot of the result of binary interpolative coding.
The combinatorial number systems always encodes integer sequences at the entropy limit.
The text was updated successfully, but these errors were encountered: