-
Notifications
You must be signed in to change notification settings - Fork 2k
Lesson 3: Hidden faces removal (z buffer)
Hello, let me introduce you my friend z-buffer of a black guy. He will help us get rid of the visual artifacts of the hidden faces removal we had during the last lesson.

By the way, i'd like to mention that this model i use heavily in the course is created by Vidar Rapp. He kindely granted me a permission to use it for teaching rendering basics and i vandalized it, but i promise you to give back the eyes to the guy.
Well, back to the topic, in theory we could just draw all the triangles without discarding any. If we do it properly starting rear-to-front, the front facets will erase the back ones. It is called the painter's algorithm. Unfortunately, it comes along with a high computational cost: for each camera movement we need to re-sort all the scene. And then there are dynamic scenes... And this is not even the main problem. The main problem is it is not always possible to determine the correct order.
Imagine a simple scene made of three triangles: the camera looks up-to-down, we project the colored triangles onto the white screen:
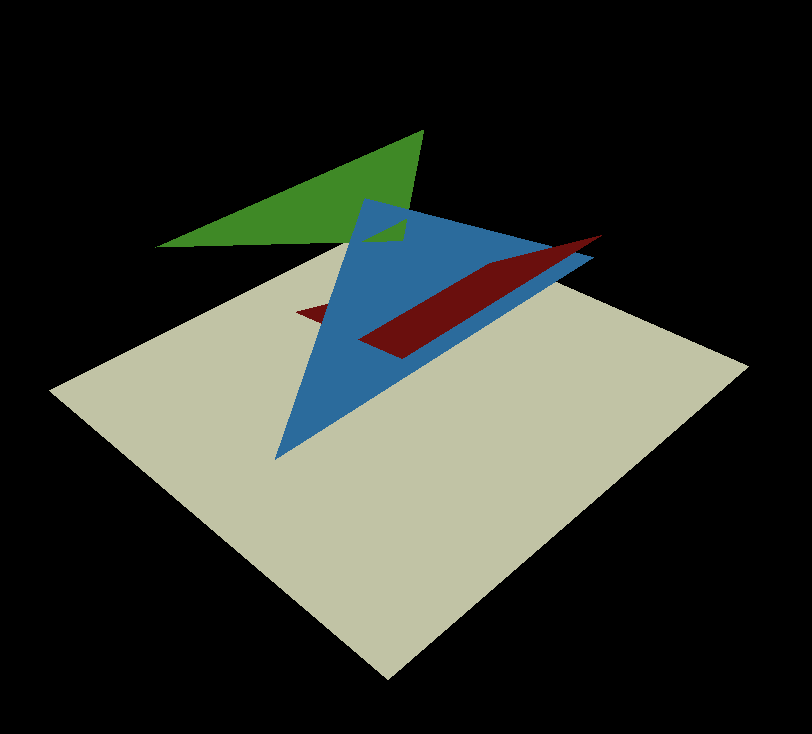
The render should look like this:

Blue facet - is it behind or in front of the red one? The painter's algorithm does not work here. It is possible to split blue facet in two (one in front of the red facet and one behind). And then the one in front of the red one is to be split in two - one in front of the green triangle and one behind... I think you get the problem: in scenes with millions of triangles it is really expensive to compute. It is possible to use BSP trees to get it done. By the way, this data structure is constant for moving camera, but it is really messy. And the life is too short to get it messy.
Let us lose a dimension for a while and to cut the above scene along the yellow plane:
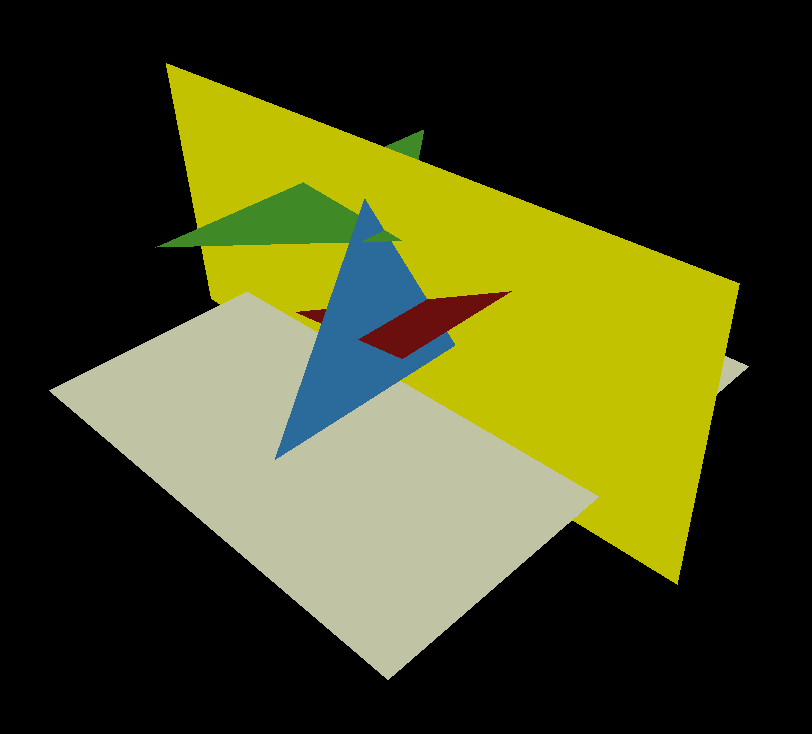
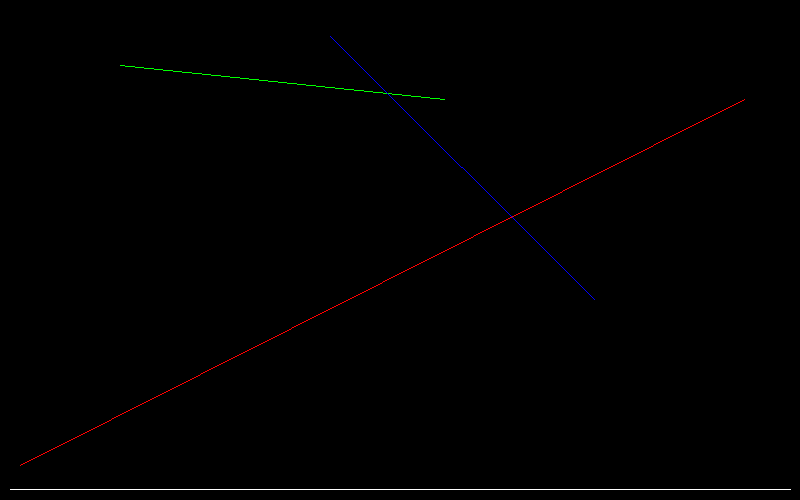
I mean, now our scene is made of three line segments (intersection of the yellow plane and each of the triangles), and the final render has a normal width but 1 pixel height:

As always, there is a commit available. Our scene is two-dimensional, so it is easy to draw it using the line() function we programmed in the very first lesson.
{ // just dumping the 2d scene (yay we have enough dimensions!)
TGAImage scene(width, height, TGAImage::RGB);
// scene "2d mesh"
line(Vec2i(20, 34), Vec2i(744, 400), scene, red);
line(Vec2i(120, 434), Vec2i(444, 400), scene, green);
line(Vec2i(330, 463), Vec2i(594, 200), scene, blue);
// screen line
line(Vec2i(10, 10), Vec2i(790, 10), scene, white);
scene.flip_vertically(); // i want to have the origin at the left bottom corner of the image
scene.write_tga_file("scene.tga");
}This is how our 2D scene looks like if we look at it sideways:
Let us render it. Recall that the render is 1 pixel height. In my source code I create images 16 pixels height for the ease of reading on high resolution screens. rasterize() function writes only in the first line of the image render
TGAImage render(width, 16, TGAImage::RGB);
int ybuffer[width];
for (int i=0; i<width; i++) {
ybuffer[i] = std::numeric_limits<int>::min();
}
rasterize(Vec2i(20, 34), Vec2i(744, 400), render, red, ybuffer);
rasterize(Vec2i(120, 434), Vec2i(444, 400), render, green, ybuffer);
rasterize(Vec2i(330, 463), Vec2i(594, 200), render, blue, ybuffer);So, i declared a magic array ybuffer with dimensions (width, 1). This array is initialized with minus infinity. Then i call rasterize() function with this array and the image render as arguments. How does the function look like?
void rasterize(Vec2i p0, Vec2i p1, TGAImage &image, TGAColor color, int ybuffer[]) {
if (p0.x>p1.x) {
std::swap(p0, p1);
}
for (int x=p0.x; x<=p1.x; x++) {
float t = (x-p0.x)/(float)(p1.x-p0.x);
int y = p0.y*(1.-t) + p1.y*t;
if (ybuffer[x]<y) {
ybuffer[x] = y;
image.set(x, 0, color);
}
}
}It is really-really simple: i iterate through all x-coordinates between p0.x and p1.x and compute the corresponding y-coordinate of the segment. Then i check what we got in our array ybuffer with current x index. If the current y-value is closer to the camera than the value in the ybuffer, then i draw it on the screen and update the ybuffer.
Let us see it step-by-step. After calling rasterize() on the first (red) segment this is our memory:
screen:

ybuffer:

Here the magenta color indicates the minus infinity, those are places corresponding to the screen we did not touch. All the rest is shown in the shades of gray: clear colors are close to the camera, dark colors far from the camera.
Then we draw the green segment.
screen:

ybuffer:

And finally the blue one.
screen:

ybuffer:

Congratulations, we just drew a 2D scene on a 1D screen! Let us admire once again the render:

So, for drawing on a 2D screen the z-buffer must be two-dimensional:
int *zbuffer = new int[width*height];Personally i pack a two-dimensional buffer into a one-dimensional, the conversion is trivial:
int idx = x + y*width;and the back one:
int x = idx % width;
int y = idx / width;Then in the code i simply iterate through all the triangles and call the rasterizer function with current triangle and a reference to the z-buffer.
The only difficulty is how to compute the z-value of a pixel we want to draw. Let us recall how we computed the y-value in the y-buffer example:
int y = p0.y*(1.-t) + p1.y*t;What is the nature of the t variable? It turns out that (1-t, t) are barycentric coordinates of the point (x,y) with respect to the segment p0, p1: (x,y) = p0*(1-t) + p1*t. So the idea is to take the barycentric coordinates version of triangle rasterization, and for every pixel we want to draw simply to multiply its barycentric coordinates by the z-values of the vertices of the triangle we rasterize:
triangle(screen_coords, float *zbuffer, image, TGAColor(intensity*255, intensity*255, intensity*255, 255));
[...]
void triangle(Vec3f *pts, float *zbuffer, TGAImage &image, TGAColor color) {
Vec2f bboxmin( std::numeric_limits<float>::max(), std::numeric_limits<float>::max());
Vec2f bboxmax(-std::numeric_limits<float>::max(), -std::numeric_limits<float>::max());
Vec2f clamp(image.get_width()-1, image.get_height()-1);
for (int i=0; i<3; i++) {
for (int j=0; j<2; j++) {
bboxmin[j] = std::max(0.f, std::min(bboxmin[j], pts[i][j]));
bboxmax[j] = std::min(clamp[j], std::max(bboxmax[j], pts[i][j]));
}
}
Vec3f P;
for (P.x=bboxmin.x; P.x<=bboxmax.x; P.x++) {
for (P.y=bboxmin.y; P.y<=bboxmax.y; P.y++) {
Vec3f bc_screen = barycentric(pts[0], pts[1], pts[2], P);
if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) continue;
P.z = 0;
for (int i=0; i<3; i++) P.z += pts[i][2]*bc_screen[i];
if (zbuffer[int(P.x+P.y*width)]<P.z) {
zbuffer[int(P.x+P.y*width)] = P.z;
image.set(P.x, P.y, color);
}
}
}
}It is terrific how little changes we made to the source code from the previous lesson to discard the hidden parts! Here is the render:

The source code can be found here.
Texture! It would be our home assignment.
In the .obj file we have lines starting with "vt u v", they give an array of texture coordinates. The number in the middle (between the slashes) in the facet lines "f x/x/x x/x/x x/x/x" are the texture coordinates of this vertex of this triangle. Interpolate it inside the triangle, multiply by the width-height of the texture image and you will get the color to put in your render.
Diffuse texture can be taken here.
Here is an example of what I expect from you: